LuoTianyi and the Floating Islands (Hard Version) 题解
题面和翻译来自洛谷,链接
题面翻译
给定一棵 $n$ 个结点的树,现在有 $k(k\le n)$ 个结点上有人。
一个结点是好的当且仅当这个点到所有人的距离之和最小。
求在这 $n$ 个点中随机取 $k$ 个点时,好的结点的期望个数,对 $10^9+7$ 取模。
样例 #1
样例输入 #1
1 | 4 2 |
样例输出 #1
1 | 666666674 |
样例 #2
样例输入 #2
1 | 5 5 |
样例输出 #2
1 | 1 |
提示
In the first example the air routes form the following tree:
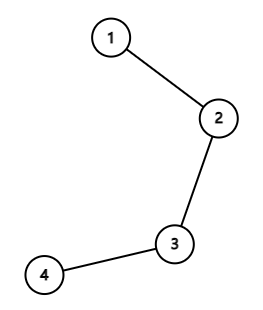 If the people are in the islands $ 1 $ and $ 2 $ , then islands $ 1 $ and $ 2 $ will be good.
If the people are in the islands $ 1 $ and $ 2 $ , then islands $ 1 $ and $ 2 $ will be good.
The sum of the distances from island $ 1 $ or $ 2 $ to all the people is $ 1+0=1 $ , which is the minimal. While the sum of the distances from island $ 3 $ to all the people is $ 2+1=3 $ , which is greater than $ 1 $ .
Like this, when the people are in island $ 1 $ and $ 3 $ , then islands $ 1,2 $ and $ 3 $ will be good.
When the people are in islands $ 1 $ and $ 4 $ , then islands $ 1,2,3 $ and $ 4 $ will be good.
When the people are in islands $ 2 $ and $ 3 $ , then islands $ 2 $ and $ 3 $ will be good.
When the people are in islands $ 2 $ and $ 4 $ , then islands $ 2,3 $ and $ 4 $ will be good.
When the people are in islands $ 3 $ and $ 4 $ , then islands $ 3 $ and $ 4 $ will be good.
So the expect of the number of the good islands is $ \frac{16}{6} $ , which equals to $ 666666674 $ modulo $ 10^9+7 $ .
题解
对于原题提示中的“So the expect of the number of the good islands is $ \frac{16}{6} $ , which equals to $ 666666674 $ modulo $ 10^9+7 $”一开始不理解,后来通过查阅资料了解到有限域除法的概念解决了此问题,同时加深了对之前学的乘法逆元的理解。
题目中要求的运算结果对$ mod=10^9+7 $取模实际上是在说明计算是在集合$\{ 0,1,2,3,…,mod-1 \}$上的有限域计算,不是日常情况下的实数域,因此要遵循有限域计算的规则,另外组合数在此情景中也是有限域上的运算了。
关于有限域的性质可查阅百度百科:有限域
在这里求数学期望中的除法运算已经不是高中数学中的实数除法了,严格意义上来讲,“除$a$”应该叫做“乘$a$的乘法逆元$a^{-1}$”,因为在有限域上$a·a^{-1}=e$,$e$为单位元。
深感自己缺乏数论知识,查资料时还找到了初等数论的高中数学选修课本,但不知为何高中时压根没见过也没学过,现在来看在许多领域基础的数论都非常有用,而且听说有些地方小学就学过一部分,其内容不难,但对拓展思维很有用。
回归本题,此题是与CF1824B1同一背景的困难版本,k的范围从$[1,min(3,n)]$变成了$[1,n]$,不难注意到k为奇数时与简单版本中k==1或k==3的情况期望都是1,k为偶数时仍按照简单版本解法dfs枚举每条边的贡献再求和,由于求的是点数量的期望,需要在最后期望值+1。
而每条边贡献由经过这条边的合法路线数决定,根据题目情景推断“好点”必须在整条路径上最中间两个点之间,也可以在最中间两个点上,因此设树上以一条边的终点 $i$ 为根的子树的节点数为 $s[i]$ ,树的总节点为 $n$ ,在子树上选 $\frac{k}{2}$ 个点,然后在此边另一边剩下的点中选 $\frac{k}{2}$ 个点,两方案数相乘即为经过这条边的合法路径总数,最终答案如下。
$$
ans = \frac{ \sum_{i=1}^{n} C_{s[i]}^{k/2} \cdot C_{n-s[i]}^{k/2} }{C_{n}^{k}} +1
$$
参考代码
1 |
|